Резник Н.А., Иванчук Н.В. Действия над рациональными выражениями

Главная -> Визуальные уроки -> Действия над рациональными выражениями

Уважаемые коллеги!
Мы с благодарностью примем
ваши замечания и предложения.
Наталья Резник (nareznik@yandex.ru),
Наталия Ежова (naegova@yandex.ru)

ДЕЙСТВИЯ НАД РАЦИОНАЛЬНЫМИ ВЫРАЖЕНИЯМИ

Резник Н.А., Иванчук Н.В.

          Тема "Дроби" чрезвычайно важна. Если по каким-то причинам алгоритмы, формируемые при их прохождении, окажутся недостаточно прочными, то под наплывом нового материала они как бы растворятся, станут тормозом для дальнейшего успешного обучения математике.
          К сожалению, данный факт наблюдается довольно часто, несмотря на то, что "Действия над арифметическими дробями" занимают много времени и учительских усилий в курсе математики 6-7 классов. Не помогает и то, что большинство задач учебников ориентировано на периодическое восстановление и закрепление необходимых навыков. Повторение надоевших правил мало способствует мотивации к обучению.
          Естественно, что при введении новых понятий или формировании новых алгоритмов восстановление необходимых навыков должно идти в несколько ином режиме, чем сам собственно процесс их формирования, иначе он может занять слишком много времени и не помочь выполнению цели. Чтобы такие уроки максимально способствовали восстановлению знаний и навыков, необходимо применять разнообразные методические приемы.
          В 1995 году нами были разработаны специальные сценарии специальных уроков для восьмых классов Мурманского морского лицея. Ниже мы приводим описание одного из них - урока, проведенного в "слабом" 8-ом технологическом классе лицея. Подчеркнем, что данный урок был строго ориентирован только на восстановление утраченных знаний и навыков. При этом мы учитывали, что повторение и закрепление необходимо строить не как дублирование уже известного, а как работу, требующую самостоятельного, творческого применения полученных знаний.
          Для предотвращения наиболее распространенных ошибок восстановление навыков мы начали с повторения действий над арифметическими дробями (рис. 1).
          Затем все вместе решали пример №1, уделяя большое внимание зрительному анализу задания (рис. 2).
          На доске были оформлены примеры, наглядно иллюстрирующие принцип сокращения дробей; определения противоположных выражений; сложения целого числа и рациональной дроби; деления дробей (рис. 3).

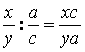
Рис. 3

          На этом вводная часть урока закончилась, и каждый лицеист получил листы с набором заданий, расположенных в определенном порядке. Некоторое время дети внимательно и заинтересованно рассматривали их.
          Подавляющее большинство лицеистов хорошо справилось с первым тестом, выполняющим пропедевтическую роль (рис. 4).
          Мы добивались, чтобы ученики приходили к нужному результату без письменного оформления промежуточных вычислений, делали это устно, определяя общие элементы информации и, производя с ними действия, выявляющие ее структуру.
          С помощью простых наблюдений было выведено правило: если общий числовой множитель имеется у всех слагаемых числителя и у всех слагаемых знаменателя арифметической дроби, то всю дробь можно сократить на этот множитель (рис. 5).
          При решении второго задания "Посмотрите и найдите" лицеисты обратили внимание на следующие вопросы (рис. 6):
      – сколько примеров нужно решить?
      – сколько действий нужно осуществить?
      – можно ли устно решить этот пример?
          Этот пример настолько заинтересовал ребят, что они не только сосредоточенно обдумывали ситуацию, но и внимательно следили за ответами своих товарищей, корректируя их ошибки.
          Далее перешли к сериям №3 и №4. Здесь шла работа на повторение и закрепление основного свойства дроби.
          В серии №3 ответ можно было получить с помощью простого сравнивания множителей числителя и знаменателя (рис. 7).
          В серии №4 подобное сравнение можно было произвести только после вынесения общего множителя (рис. 8).
          Выведенное ранее правило теперь выглядело так: если общий множитель имеется у всех слагаемых числителя и у всех слагаемых знаменателя алгебраической дроби, то его также можно “погасить” (рис. 9).
          Затем был рассмотрен необычный пример №5 (рис. 10). Учащиеся с удовольствием рассматривали “ручки”, обсуждали правила умножения, исследовали строку ответов и находили правильный результат. Этот тест был введен для того, чтобы дети научились переводить вербальное описание преобразований в визуальный план действий, поддерживая ход мыслительных операций стрелками-указателями.
          После этого обратились к информационной странице “Действия над взаимно обратными выражениями” и внесли недостающую информацию в общие схемы алгоритмов действий над алгебраическими дробями (рис. 11).
          Теперь лицеисты могли использовать эту схему как справочник при решении теста №7 (рис. 12).
          Один из правильных ответов в тесте №8 был преднамеренно опущен для того, чтобы нацелить учащихся не на подгонку, а на действительное получение верных результатов (рис. 13).
          Тест №9 оказался весьма поучительным (рис. 14). Многие решили сначала подставить цифры, а затем уже приступать к преобразованиям. Некоторые начали именно с упрощений выражений. Победило меньшинство. Сравнили возможные пути решения, и пришли к выводу: полезнее сначала упростить алгебраическую дробь, а затем уже находить ее значение при определенных условиях.
          В завершение урока была предложена небольшая самостоятельная работа по заданиям матрицы (рис. 15). Лицеисты выполняли примеры строки или столбца, записывая ответы в соответствующей пустой клетке, результаты работы показали, что все учащиеся успешно справились с ней.
          Разнообразные по содержанию и сложности задания способствовали высокой активности учащихся и продуктивности урока. Не было ни одного лицеиста, не вовлеченного в процесс поиска результатов. Слабые ученики, не стесняясь, высказывали свои мысли. Они не боялись делать ошибки, старались сами их определить и исправить.
          Таким образом, восстановление утраченных знаний и навыков на данном этапе прошло успешно и помогло в дальнейшей работе по приобретению новых навыков.

Скачать комплект визуальных дидактических материалов по теме данной статьи.

Литература

Резник Н.А. Визуальные уроки. Компл. дидакт. матер. к шк. урокам. - СПб.: Свет, 1996.
Иванчук Н.В., Резник Н.А. Восстановление утраченных знаний и навыков //Математика в школе. - 1996. - №6.

Авторефераты | Визуальные уроки |Библиография