Линейные преобразования параболы и гиперболы

Главная -> Визуальные дидактические материалы -> Математика ->Алгебра->
Линейные преобразования параболы и гиперболы

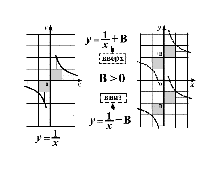
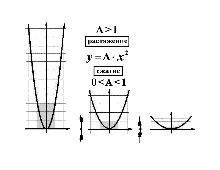
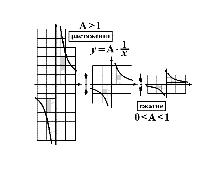
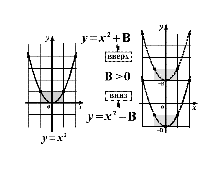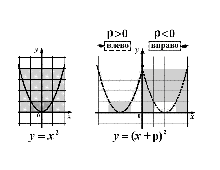Визуальные дидактические материалы
«Линейные преобразования параболы и гиперболы»

Cлайд-фильмы серии «Линейные преобразования параболы и гиперболы» коллекции «Формулы и графики»
предназначены для формирования начальных представлений о линейных преобразованиях графиков элементарных функций. Прилагаются также образцы дидактических материалов для самостоятельной работы учащихся (рекомендуется распечатка).

Эти фильмы могут быть воспроизведены на любом компьютере с WINDOWS версии 95 (и выше) без дополнительной установки специальных программ, так как выполнены в формате ЕХЕ.

Принцип управления: переход между кадрами (слайдами) осуществляется нажатием рисованной (графической) кнопки. Движение возможно как “вперед”, так и “назад”.

Слайд-фильмы предназначены для группового обучения и могут быть использованы учителем непосредственно на школьных уроках. Предлагаемый нами принцип управления фильмом позволяет останавливаться на кадрах, требующих специального внимания.

Линейные преобразования параболы и гиперболы
	1. Направляющие прямоугольники параболы 2. Направляющие прямоугольники гиперболы 3. Сдвиги по оси ординат направляющих прямоугольников параболы 4. Сдвиги по оси ординат направляющих прямоугольников гиперболы 5. Деформация по оси ординат направляющих прямоугольников параболы 6. Деформация по оси ординат направляющих прямоугольников гиперболы 7. Сдвиги по оси абсцисс направляющих прямоугольников параболы
Краткое содержание серии

№1. Направляющие прямоугольники параболы

Кадр из фильма

Фильм показывает, как на клетчатой бумаге без лекал можно достаточно точно построить параболу – график функции y=x².

Полезно обратить внимание учащихся на удобные для построения направляющие малый и большой прямоугольники, визуально заменяющие привычную таблицу значений квадратичной зависимости y=x² в точках х= -2;-1;0;1;2.

Просмотр слайд-фильма

Дидактическое приложение

К списку фильмов

№2. Направляющие прямоугольники гиперболы
	Фильм показывает, как на клетчатой бумаге без лекал можно достаточно точно построить гиперболу – график функции y=1/x. Полезно обратить внимание учащихся на удобные для построения направляющие квадраты, вертикальные и горизонтальные прямоугольники, визуально заменяющие привычную таблицу значений обратной пропорциональной зависимости y=1/x в точках х= -2;-1;0;1;2.
Просмотр слайд-фильма	Дидактическое приложение	К списку фильмов

№3. Сдвиги по оси ординат направляющих прямоугольников параболы

Фильм показывает, как, на основе уже изученных приемов построения параболы легко произвести ее перемещения вдоль оси ординат.

Следует обратить внимание учащихся на связь между знаком числового параметра В в задании функции y=x²±В и расстоянием, на которое перемещается график функции y=x² вместе с его направляющими прямоугольниками.

Просмотр слайд-фильма

Дидактическое приложение

К списку фильмов

№4. Сдвиги по оси ординат направляющих прямоугольников гиперболы

Кадр из фильма

Фильм показывает, как, на основе уже изученных приемов построения гиперболы, легко произвести ее перемещения вдоль оси ординат.

Следует обратить внимание учащихся на связь между знаком числового параметра В в задании функции y=1/x±В и расстоянием, на которое перемещается график функции y=1/x вместе с его направляющими прямоугольниками.

Просмотр слайд-фильма

Дидактическое приложение

К списку фильмов

№5. Деформация по оси ординат направляющих прямоугольников параболы

Кадр из фильма

Фильм показывает, как с помощью сжатия (растяжения) направляющих прямоугольников легко выполнить деформацию графика параболы вдоль оси ординат.

Следует обратить внимание учащихся на связь между знаком числового параметра А в задании функции y=А^.x² и растяжением или сжатием, которому подвергается график исходной функции y=x² вместе с его направляющими прямоугольниками в зависимости от значения параметра А.

Просмотр слайд-фильма

Дидактическое приложение

К списку фильмов

№6. Деформация по оси ординат направляющих прямоугольников гиперболы

Кадр из фильма

Фильм показывает как с помощью сжатия (растяжения) направляющих прямоугольников легко выполнить деформацию графика гиперболы вдоль оси ординат.

Следует обратить внимание учащихся на связь между знаком числового параметра А в задании функции y=А/x и растяжением или сжатием, которому подвергается график исходной функции y=1/x вместе с его направляющими прямоугольниками в зависимости от значения параметра А.

Просмотр слайд-фильма

Дидактическое приложение

К списку фильмов

№7. Сдвиги по оси абсцисс направляющих прямоугольников параболы

Кадр из фильма

Фильм показывает, как с помощью гипотез можно на основе уже изученных приемов исследований сформировать алгоритм перемещения параболы вместе с ее направляющими прямоугольниками вдоль оси абсцисс.

Следует обратить внимание учащихся на связь между знаком числового параметра р в задании функции y=(x±р)² и расстоянием, на которое перемещается график функции y=x² вместе с его направляющими прямоугольниками.

Просмотр слайд-фильма

Дидактическое приложение

К списку фильмов

Авторский коллектив:

Концепция и визуализация - Резник Н.А.

Проектирование и визуальная организация - Ежова Н.М.

Тестирование и апробация - Иванчук Н.В.

Математическое редактирование - Шупова Г.М. и Карпова О.П.

Главная -> Визуальные дидактические материалы -> Математика-> Алгебра->
Линейные преобразования параболы и гиперболы