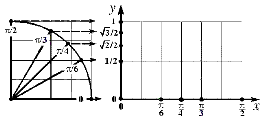Первая четверть тригонометрической окружности

Главная -> Визуальные дидактические материалы -> Математика -> Тригонометрия->
Первая четверть тригонометрической окружности

Уважаемые коллеги!
Мы с благодарностью примем
ваши замечания и предложения.
Наталья Резник (nareznik@yandex.ru),
Наталия Ежова (naegova@yandex.ru)

Визуальные дидактические материалы
«Первая четверть тригонометрической окружности»

Серия «Первая четверть тригонометрической окружности» коллекции «Тригонометрическая окружность»
предназначена для формирования начальных представлений о важнейших понятиях тригонометрии.
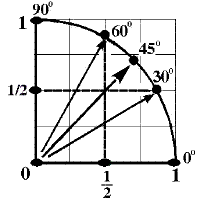
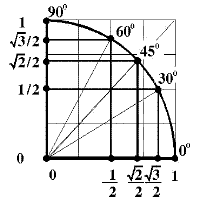
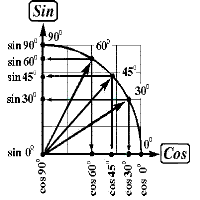
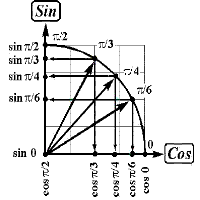
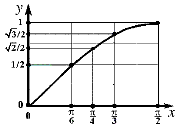
Главная цель заключается в том, чтобы учащиеся увидели, какие, где и как можно увидеть «замечательные числа», переходя затем к построению и визуальному определению соотношений этим числам синусов и косинусов замечательных углов;узнали, какую роль играют «замечательные точки» при построении графика функции на промежутке от 0 до П/2.

Эти фильмы могут быть воспроизведены на любом компьютере с WINDOWS версии 95 (и выше) без дополнительной установки специальных программ, так как выполнены в формате ЕХЕ.

Принцип управления: переход между кадрами (слайдами) осуществляется нажатием рисованной (графической) кнопки. Движение возможно как “вперед”, так и “назад”.

Слайд-фильмы предназначены для группового обучения и могут быть использованы учителем непосредственно на школьных уроках. Предлагаемый нами принцип управления фильмом позволяет останавливаться на кадрах, требующих специального внимания.

Первая четверть тригонометрической окружности
	1. Замечательные углы первой четверти тригонометрической окружности 2. Замечательные радикалы на радиусах первой четверти тригонометрической окружности 3. Замечательные синусы и косинусы углов первой четверти тригонометрической окружности 4. Радианная мера замечательных углов первой четверти тригонометрической окружности 5. Замечательные радианы и радикалы первой четверти тригонометрической окружности 6. График синуса на промежутке от 0 до П/2 на клетчатой бумаге 7. График косинуса на промежутке от 0 до П/2 на клетчатой бумаге
Краткое содержание серии

№1. Замечательные углы первой четверти тригонометрической окружности

Кадр из фильма

Фильм показывает, как на клетчатой бумаге с помощью ручки и циркуля можно без транспортира достаточно точно построить замечательные углы.

Полезно обратить внимание учащихся на удобные для вычислений и соответствующих построений значения замечательных углов, под которыми понимаются углы 0, 30, 45, 60 и 90 градусов первой четверти тригонометрической окружности.

Проверено: вирусов нет!
Просмотр слайд-фильма

К списку фильмов

№2. Замечательные радикалы на радиусах первой четверти тригонометрической окружности
	Фильм показывает, как на клетчатой бумаге с помощью вспомогательных прямоугольников достаточно просто отметить некоторые особые числа, которые здесь именуются замечательными радикалами, на радиусах тригонометрической окружности. Полезно обратить внимание учащихся на удобные для вычислений и соответствующих построений значения замечательных радикалов, являющихся координатами точек, образующихся на первой четверти тригонометрической окружности при построении ее замечательных углов.
Проверено: вирусов нет! Просмотр слайд-фильма	К списку фильмов

№3. Замечательные синусы и косинусы углов первой четверти тригонометрической окружности

Фильм показывает, как, на основе уже изученных приемов, легко определить значения синусов и косинусов замечательных углов

Следует обратить внимание учащихся на связь между замечательными углами первой четверти тригонометрической окружности и соответствующими им замечательными синусами и косинусами, под которыми подразумеваются синусы и косинусы замечательных углов

Проверено: вирусов нет!
Просмотр слайд-фильма

К списку фильмов

№4. Радианная мера замечательных углов первой четверти тригонометрической окружности

Кадр из фильма

Фильм показывает, как на линии синуса и косинуса отметить синусы и косинусы замечательных углов первой четверти тригонометрической окружности, выраженных в радианах. Кроме того происходит сопоставление равных значений замечательных синусов и косинусов для разных углов.

Следует обратить внимание на то, как связаны между собой радианная и градусная меры замечательных углов

Проверено: вирусов нет!
Просмотр слайд-фильма

К списку фильмов

№5. Замечательные радианы и радикалы первой четверти тригонометрической окружности
	Фильм показывает, как на клетчатой бумаге с помощью модели первой четверти тригонометрической окружности легко с достаточной степенью точности определить положение замечательных радиан и радикалов на осях специальной тригонометрической системы координат.
Проверено: вирусов нет! Просмотр слайд-фильма	К списку фильмов

№6. График синуса на промежутке от 0 до П/2 на клетчатой бумаге

Кадр из фильма

Фильм показывает как с помощью замечательных точек первой четверти тригонометрической окружности можно на клетчатой бумаге построить график синуса на промежутке от 0 до П/2.

Предполагается дать учащимся первичные представления о построении в тригонометрической системе координат графика синуса, который определяется как кривая, проходящая через замечательные точки синуса.

Проверено: вирусов нет!
Просмотр слайд-фильма

К списку фильмов

№7. График косинуса на промежутке от 0 до П/2 на клетчатой бумаге

Кадр из фильма

Фильм показывает, что построение замечательных косинусов на клетчатой бумаге также происходит на оси значений тригонометрической функции. Аналогично замечательные радианы первой четверти тригонометрической окружности откладываются на оси значений ее аргумента.

Предполагается дать учащимся первичные представления об особенностях построении в тригонометрической системе координат графика косинуса, который также определяется как кривая, проходящая через его замечательные точки.

Проверено: вирусов нет!
Просмотр слайд-фильма

К списку фильмов

Авторский коллектив:

Концепция и визуализация - Резник Н.А.

Проектирование и визуальная организация - Ежова Н.М.

Тестирование и апробация - Шубина Т.В.

Математическое редактирование - Шупова Г.М. и Карпова О.П.

Материал предоставляется для свободного некоммерческого использования
с обязательной ссылкой на авторов (согласно ст. 1229 Гражданского кодекса РФ).

Главная -> Визуальные дидактические материалы -> Математика-> Тригонометрия->
Первая четверть тригонометрической окружности