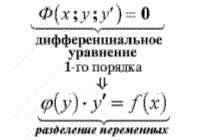|

|
Данько Оксана
Физико-математический факультет,
специальность Математика-Физика,
5-й курc (ноябрь 2009)
|
|
|
О дидактических материалах
«Действия над рациональными выражениями»
и
«Многоэтажные дроби»
Данные дидактические материалы очень помогают не только на уроках и при их подготовке, но и при индивидуальной работе с учащимися (репетиторстве).
Я хочу рассказать, как помогли мне эти дидактические материалы.
Я занималась репетиторством с учеником 8 класса (учебник Мордкович А.Г.), который практически не усвоил
программу 7 класса по алгебре и, как результат, не мог освоить программу 8 класса,
т.е. по математике мальчик был очень запущен.
Чтобы объяснить тему 8 класса «Действия с алгебраическими дробями»
надо было выучить темы 7 класса «Действия с обыкновенными дробями»,
«Преобразование многочленов», «Формулы сокращённого умножения» и т.д.
В данной ситуации,
чтобы ребенок заучивал что-либо, не хотелось, из-за этого мог сразу пропасть интерес к занятиям.
Поэтому дидактические материалы очень выручили меня здесь.
|
Во-первых, их простая и схематичная форма
объяснения материала, к
оторая помогает зрительно запомнить, как выполняется то или иное действие.
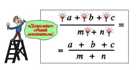
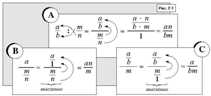
Во-вторых, материалы содержат целых комплект заданий, которые готовы к применению, т.е. их можно распечатать
и выполнять прямо на этом листе, при этом не бояться сделать ошибку (если работать карандашом) (рис. 2-1)
(Дидактические материалы
«Действия над рациональными выражениями» и
«Многоэтажные дроби»).
|
|
В-третьих, необычные задания («Шторм на море», «Полицейские и воры»)
в игровой форме помогают активизировать мыслительную деятельность,
после чего выполнение этого задания с числами становится понятнее и легче.
Наглядные иллюстрации, схемы, тесты и вообще весь комплект визуальных дидактических материалов
восстановили утраченные навыки и помогли в дальнейшей работе.
К списку отзывов
|
|
|

|
Мартынова Елена
Физико-математический факультет,
специальность Математика-Физика,
5-й курc (ноябрь 2009)
|
О серии
«Дифференциальные уравнения 1-го порядка с разделяющимися переменными»и
«Однородные дифференциальные уравнения 1-го порядка»
коллекции «Начальные представления о дифференциальных уравнениях 1-го порядка с произвольными коэффициентами»
Темы по дифференциальным уравнениям с разделяющимися
переменными – самые простые.
В Internet по дифференциальным уравнениям я не нашла (ноябрь 2009 г.) ничего.
Только голая теория: нет ни задач, ни упражнений, ничего...
Есть только в Экспоненте (exponenta.ru) примеры и задания:
сделать и проверить себя. Но там три примера и все.
Но теория есть и в учебниках.
В слайд-фильмах всё наоборот.
Здесь сразу всё понятно, все структурировано
Несмотря на их простоту, они не смотрятся как детские, в них не теряешься, как в теории,– все разложено по полочкам.
На каждом слайде – нужная конкретная информация.
И хорошо, что
не все диф. уравнения сразу, а по пунктам:
с разделяющимися переменными:
1.Решение дифференциальных уравнений 1-го порядка (рис. 1.1)
2.Дифференциальные уравнения с разделяющимися переменными (рис. 1.2)
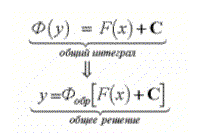
3.Общий интеграл и общее решение дифференциального уравнения
с разделяющимися переменными (рис. 1.3)
4.Разделение переменных в уравнениях с дифференциалами (рис. 1.4)
5.Частные решения дифференциальных уравнений
1-го порядка с разделяющимися переменными (рис. 1.5)
|

|
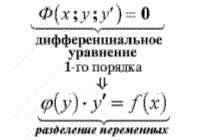
|
|
|
Рис. 1.1
|
Рис. 1.2
|
Рис. 1.3
|
|

|
|

|
|
Рис. 1.4
|
|
Рис. 1.5
|
oднородные:
- Однородные дифференциальные уравнения 1-го порядка (рис. 2.1)
- Алгоритм нахождения решений однородных дифференциальных уравнений 1-го порядка (рис. 2.2)
- Нахождение частных решений однородных дифференциальных уравнений 1-го порядка (рис. 2.3)
и т.д.
|
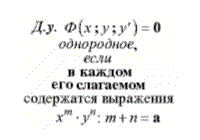
|

|

|
|
Рис. 2.1
|
Рис. 2.2
|
Рис. 2.3
|
Всё выстроено так, что одно вытекает из другого.
И еще:
на каждом кадре материал так ясно изложен, так мало
информации, что не успеваешь ее забыть, переходя к следующему
кадру.
К списку отзывов
|
|

|
Рангулов Артём
Физико-математический факультет,
специальность Математика-Информатика,
3-й курc (декабрь 2009)
|
|
|
|
О слайд-фильмах Визуальной школы
Слайд-шоу серии «Нахождение производной функции по её определению»
коллекция «Начальные представления о технике дифференцирования» подходят для обучения школьников и студентов.
Они обладают понятным интерфейсом и простотой цветовой гаммы.
Отвлекающие элементы отсутствуют. Знак "?" заставляет пользователя задуматься над решением задачи и прорешать самостоятельно, и в итоге сравнить.
В слайд-шоу «Написание и чтение символа и формулы производной функции в заданной точке» есть небольшая предыстория и даны ученые.
Недостатки: Сложно попасть на кнопку перехода на другой слайд. Надо либо сделать побольше кнопку, либо просто щелкать по слайдам.
Недостатки сайта www.vischool.rxt.ru
- тусклый фон начальной страницы сайта (серые и коричневые оттенки)
- мало картинок
К списку отзывов
|
|
|