При повторении и закреплении пройденного многие учителя, наряду со стандартными примерами, вводят задания повышенной сложности, ожидая определенного прироста умений и навыков.
Однако в большинстве случаев этот прогноз не оправдывается. Повторение зачастую оказывается скучным, и ученики неохотно решают надоевшие им примеры и задачи.
Например, тема “Действия над алгебраическими дробями” занимает много времени в школьном курсе математики 7 и 8 классов. Тем не менее значительная часть учеников часто путается и ошибается, огорчая учителя и получая за свою работу плохие оценки. Не помогает и то, что большинство задач школьных учебников ориентированы на периодическое восстановление и закрепление этих навыков. Повторение надоевших правил мало способствует мотивации к обучению.
В Мурманском морском лицее в 8 судомеханическом классе эта проблема
решалась следующим образом. Констатировав, что сокращение дробных выражений постоянно вызывает у лицеистов затруднения,
было решено вновь “зажечь огонёк интереса” с помощью особого приема.
После непродолжительного самостоятельного изучения
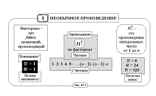
информационной страницы “Необычное произведение” (рис. 47-1) ученики приступили к тренажерам
(рис. 47-2).Первый из них (рис. 47-2, слева)
привлёк внимание к возможным сочетаниям выражений, внешне содержащих одни и те же числовые величины.
Второй (рис. 47-2, в центре)
тренажёр помог увидеть возможность выражения n–факториал через (n–1)-факториал.
В ходе короткого спора вывели: n! = (n–1)! · n.
Следующие упражнения (рис. 47-2, справа) закрепили технику расшифровки нового символа.
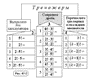
Тест № 5 (рис. 47-3) решили быстро.
 Pис. 47-1 |
 Pис. 47-2 |
 Pис. 47-3 |
 Pис. 48-1 |
 Pис. 48-2 |
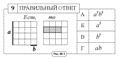 Pис. 48-3 |
 Pис. 48-4 |
Скачать комплект
визуальных дидактических материалов по теме данной статьи.
Предлагаемые комплекты дидактических материалов на экране отражаются не совсем точно,
но распечатываются рисунки прекрасно!
Уважаемые коллеги!
Мы с благодарностью примем
ваши замечания и предложения.
Наталья Резник (nareznik@yandex.ru),
Наталия Ежова (naegova@yandex.ru)