Традиционно в школе впервые знакомятся с синусом, косинусом и тангенсом острого угла в 8-м классе.
Определения их вводятся через отношения в прямоугольном треугольнике. Такое представление трудно воспринимается и запоминается восьмиклассниками,
– отсутствует опора на зрительное восприятие данных объектов. Мы решили пойти несколько иным путём: попытаться дать детям возможность «увидеть» синус и косинус, тангенс и котангенс угла.
Естественно, что такому подходу должен был предшествовать подготовительный период. Заранее познакомились с тригонометрической окружностью.
Особое внимание было уделено части окружности в первой координатной четверти. Научились строить
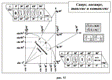
на окружности углы 0o, 30o, 45o, 60o, 90o без транспортира,
вспомнив свойства углов и сторон прямоугольного треугольника с такими углами. Эти
углы мы назвали «замечательными» (рис. 1).
С помощью теоремы
Пифагора определили «замечательные» на осях координаты (то есть координаты точки тригонометрической окружности, соответствующей данному углу).
Учащиеся сами заметили закономерность в последовательности чисел на осях (рис. 2). Затем перешли к «замечательным» числам на правой и верхней касательных. Используя интуитивные представления о подобии
прямоугольных треугольников, составили соответствующие пропорции, и нашли числа на касательных (рис. 3).
) Рис.1 |
) Pис. 2 |
) Pис. 3 |
Целью данного урока являлось:
1) вывести самостоятельно понятия синуса, косинуса, тангенса и котангенса острого угла;
2) научиться находить значения синусов и косинусов острых углов, используя тригонометрическую окружность;
3) выработать навык изображения и измерения тангенсов и котангенсов острых углов.
Урок состоял из следующих этапов:
1.Повторение правил построения «замечательных» углов и точек
на тригонометрической окружности, соответствующих этим углам, а также нахождения их координат.
2.Введение нового материала – понятий синуса и косинуса острого угла.
3.Формирование навыков по нахождению синусов и косинусов острых углов.
4.Введение понятий тангенса и котангенса острого угла.
5.Формирование умений изображать и измерять тангенсы и
котангенсы острых углов, навыков вычисления тангенсов и котангенсов «замечательных» углов.
6.Обобщение.
На первом этапе урока мы восстановили на доске первую четверть тригонометрической окружности, повторили, какие углы можно
построить без транспортира, нашли декартовы координаты точек окружности, соответствующих «замечательным» углам (рис. 2).
|
На втором этапе урока ввели обозначения и наименования координат точек на окружности, связанных с острым углом α.
Для этого рассмотрели и обсудили рисунки на странице «Косинус острого угла» (рис. 4),
определили косинус острого угла как абсциссу точки тригонометрической окружности, соответствующей заданному углу. Изучение материала данной страницы происходило в довольно медленном темпе, так как обсуждались все детали рисунков, обращалось внимание учащихся на выполнение каждого задания. |
) Pис. 4 |
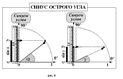
Приступили к выполнению специальных упражнений. В задании 1 (рис. 5.а) было предложено отметить угол α., заштриховать полоску, соответствующую синусу этого угла и с её помощью определить величину синуса угла α. Класс сразу втянулся в поиск. Упражнение очень понравилось лицеистам, они с удовольствием выполняли его, с интересом проверяли ответы, радовались, что не допустили здесь ни одной ошибки. Это настроило их на успех, на то, что новый материал совсем нетрудный. При рассмотрении страницы «Синус острого угла» (рис. 6) учащиеся самостоятельно определили синус острого угла как ординату точки тригонометрической окружности, соответствующей заданному углу. При помощи изображённой на рисунке линейки нашли значения синусов углов. Задание на рис. 5.б в аналогично соседним заданиям слева, поэтому учащимся было предложено выполнить в классе примеры 1 и 3, а остальное сделать дома. Перед выполнением примеров последней колонки (рис. 5.в) необходимо было определить сходство и различие между выделенными треугольниками, потом произвести сравнение с рисунками предыдущего задания того же блока.
){kind=small} Pис. 5.а |
){kind=small} Pис. 5.б |
) Pис. 5.в |
) Pис. 6 |
Далее учащимся надо было ответить, как они находили синус острого угла. После обсуждения всех предположений,
ребята установили, что в каждом случае находилась ордината конца радиуса тригонометрической окружности, образующего угол α .
Так как учащиеся самостоятельно пришли к этому выводу, то задания последнего столбца (рис. 5.в) у основной массы не вызвали затруднений.
Быстро выполнили примеры под нечётными номерами, чётные – остались для домашнего задания.
|
Очень подробно остановились на странице «Линии синусов и косинусов» (рис. 7, слева).
Установили связи между декартовыми и тригонометрическими координатами, вывели правило записи тригонометрических координат.
В результате пришли к выводу: так как на оси абсцисс находят только косинусы углов, то эту ось можно назвать линией косинусов.
Ось ординат соответственно назвали линией синусов. Особое внимание было уделено тому, что и синус, и косинус угла – это конкретные числа |
) Рис. 7 |
Некоторые настолько увлеклись, что выполняли задания с опережением. Ученики, которые затруднялись при решении определённых задач, могли в это время получить помощь учителя. Поэтому все дети были поглощены работой, каждый занимался в индивидуальном темпе, при этом с неугасающим желанием и радостью от своих, пусть небольших, успехов.
На четвёртом этапе ввели понятия тангенса и котангенса острого угла.
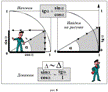
Приступив к странице «Правая касательная и тангенсы» (рис. 8), мы назвали отношение синуса
острого угла к его косинусу тангенсом данного угла.
Внимательно рассмотрев рисунки, ребята установили, что полученные треугольники подобны.
Составили соответствующие пропорции и убедились в справедливости данного равенства. Обсудили, что тангенс
острого угла – это число, соответствующее длине отрезка правой касательной, заключённого между сторонами данного угла.
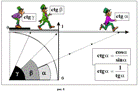
Страницу «Изображение и измерение котангенсов» (рис. 9) восьмиклассники рассмотрели самостоятельно, после чего прочитали теоретический материал
внизу страницы и сделали вывод, что тангенс и котангенс одного и того же угла – взаимно-обратные величины.
Перейдя к странице «Линии тангенсов и котангенсов» (рис. 10), мы, рассматривая человечков, немного повеселись, и разобрались, почему же они изображены различными по размеру. Оказалось, что они шагают по верхней касательной и поднимаются по правой касательной,
и что при увеличении угла, значения тангенсов углов увеличиваются, а значения котангенсов – напротив, уменьшаются.
) Pис. 8 |
) Pис. 9 |
) Pис. 10 |
){kind=small} Pис. 11.а |
){kind=small} Pис. 11.б |
) Pис. 11.в |
|
Пятый этап был связан с выработкой умений и навыков по применению полученных знаний к решению практических задач.
Этот этап урока прошёл в очень быстром темпе, так как дети уже вышли на новый уровень самостоятельности,
на новый виток в приобретении знаний: активную поисковую деятельность. |
) Pис. 12 |
После изучения темы «Синус, косинус, тангенс и котангенс острого угла»
на последующих занятиях перешли к рассмотрению данных понятий через отношения в прямоугольном треугольнике. Прежде чем говорить об отношениях в треугольнике, необходимо было
остановиться на повторении понятия отношения, так как опыт показывает, что учащиеся плохо понимают смысл этого слова.
Довольно быстро вспомнили арифметическую запись отношения.
Первый пример тренажёра (рис. 13) был разобран в классе, остальные было предложено выполнить дома.
Рассмотрели пример отношения длин сторон треугольника. Обсудили особенности задания отношений сторон
в прямоугольном треугольнике. Тренажёр № 1 (рис. 14) позволил быстро повторить различные
способы обозначения сторон прямоугольного треугольника.
Далее приступили к выполнению упражнения № 3 «Посмотрите и …»
(рис. 15), в котором повторялось свойство
биссектрисы угла треугольника, изученное ранее в теме «Подобие треугольников» тоже по визуальным материалам.
Дети выполнили его моментально.
) Pис. 13 |
) Pис. 14 |
) Pис. 15 |
Поиск правильных вариантов
заданий № 2 и 3 “Выберите ответ” (рис. 16) очень увлёк учащихся,
так как здесь требовалось внимательно рассмотреть рисунок и само отношение.
В задании “Посмотрите и…” № 4-7 (рис. 17) прямоугольный треугольник располагается таким образом,
чтобы один из его острых углов был в центре тригонометрической окружности. Предполагалось, что, зная длины сторон треугольника (а необходимые стороны выделены жирно), учащиеся будут составлять соответствующие
пропорции для нахождения значений данных отношений. Но лицеисты сначала по данным числам находили величину угла (и это послужило,
причём спонтанно, пропедевтикой к изучению дальнейшего материала).
Ученики составляли “многоэтажные” дроби, сокращали общие множители и применяли изученный ранее алгоритм преобразования такой дроби.
Таким образом, параллельно повторили и закрепили навыки преобразования многоэтажных дробей.
) Pис. 16 |
) Pис. 17 |
|
Затем перешли
к изучению страницы “Синус и косинус острого угла треугольника” (рис. 18). |
) Pис. 18 |
) Pис. 19 |
){kind=small} Рис. 20.1 |
){kind=small} Рис. 20.2 |
){kind=small} Рис. 20.3 |
){kind=small} Рис. 20.4 |
){kind=small} Рис. 20.5 |
Особое внимание уделялось задачам,
связанным с дополнительными построениями (рис. 21.1-21.3).
Как и ранее, это осуществлялось с помощью поэтапного перехода от рисунков,
полностью обеспечивающих набор данных, до таких, где эти данные
надо было выявить с помощью несложных дополнений.
Например, в серии 2 (рис. 21.а) самым сложным
оказалось пятое задание, так как здесь не было треугольника и его надо было достроить самостоятельно.
Не все учащиеся сразу справились с этим примером. После подробного анализа учащиеся смогли решить
эту задачу даже несколькими способами.Задания тренажера №1 (рис. 21.б) позволили
проверить прочность усвоения нового понятия.
Упражнения №2-№4 (рис. 21.в) были нацелены на
формирование навыков визуального поиска.
Дети увлеченно и с большим интересом искали нужные треугольники и определяли значения искомых величин.
){kind=small} Pис. 21.а |
){kind=small} Pис. 21.б |
) Pис. 21.в |
Таким образом, мы пришли к выводу,
что при введении обсуждаемых понятий как координат тригонометрической окружности появляется возможность
значительно расширить запас сведений – добавляется котангенс острого угла, обсуждаются значения синусов, косинусов, тангенсов и котангенсов углов в 0 и 90 градусов.
Плюс к этому проведена большая подготовительная работа к изучению геометрии в 9-м классе и тригонометрии в 10-м.
Лицеисты не только “увидели” синус и косинус угла, но и сами вывели определения синуса и косинуса острого угла прямоугольного треугольника.
И это произошло отнюдь неформально. При таком подходе ученики участвуют в процесс поиска и сами “открывают” новые для них знания. Так как новый материал
был тесно связан с ранее изученными и повторенными темами (тригонометрическая окружность, подобие треугольников, “многоэтажные” дроби), то он легко воспринимался учащимися.
Уважаемые коллеги!
Мы с благодарностью примем
ваши замечания и предложения.
Наталья Резник (nareznik@yandex.ru),
Наталия Ежова (naegova@yandex.ru)
