Довольно редко в обычных (и даже элитных) школах имеются классы с однородным (по уровням интеллекта и математической подготовки) составом учащихся. Привычная картина такова: есть “сильные и слабые” ученики, которые, обучаясь по одной общей программе и, получая, как правило, одни и те же задания, приходят к “финишу” с разными результатами.
Вопросы разноуровнего обучения в одном и том же классе волнуют современных учителей, поскольку такое обучение еще недостаточно обеспечено соответствующими дидактическими материалами.
Здесь предлагается модель “двухуровневого” итогового занятия, реализованного в начале октября 1995 года в 9 экономическом классе Мурманского морского лицея. На практических занятиях по математике данный класс делится на две группы, неравных по возможностям и математической подготовке лицеистов. Исходя из этого подготавливаемые для урока материалы были обработаны и оформлены так, чтобы каждая группа получала свой индивидуальный комплект задач (см. дидактическое приложение).
В обоих вариантах имеются “параллельные” задания. Так, например, “Задача о дельфинах” присутствует в каждом случае, отличаясь видом, оформлением и, как следствие, уровнем сложности вопроса к ней.
| Более легкий вариант осуществлен в виде “Правильного ответа” (рис. 68-1). | Второй вариант “Посмотрите и найдите” решить сложнее (рис. 69-1). |
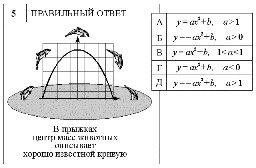 Рис. 68-1 |
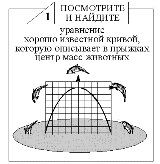 Рис. 69-1 |
В первом случае список ответов “наталкивает” учащегося на правильный ход мысли,
во втором – все преобразования учащийся должен осуществить совершенно самостоятельно,
ориентируясь только на образ квадратичной функции, представляющей траекторию прыжка животного.
 Рис. 68-2 |
 Рис. 69-2 |
Задачи “Посмотрите и определите” также не совпадают (внизу на рис. 68-3 и рис. 69-3).
Главное отличие:
в одном случае нужно проанализировать хорошо уже известный образ параболы (рис. 68-3),
во втором – следует провести серьезный и глубокий анализ формулы,
провести соответствующие исследования, позволяющие
определить новые для лицеистов свойства квадратичной функции и т.д. (рис. 69-3).
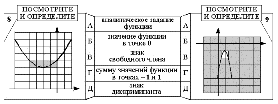 Рис. 68-3 |
 Рис. 69-3 |
Подобный подход позволяет учитывать требования разноуровневого обучения при полном соблюдении требований инвариантной части школьного курса, ориентируясь на подготовку и возможности учащихся.
Скачать комплект
визуальных дидактических материалов по теме данной статьи.
Предлагаемые комплекты дидактических материалов на экране отражаются не совсем точно,
но распечатываются рисунки прекрасно!
Уважаемые коллеги!
Мы с благодарностью примем
ваши замечания и предложения.
Наталья Резник (nareznik@yandex.ru),
Наталия Ежова (naegova@yandex.ru)