Визуальное представление математических
понятий, зрительное восприятие их свойств,
связей и отношений между ними позволяют достаточно быстро и наглядно развернуть перед
учащимися отдельные фрагменты теории,
акцентировать внимание на узловых моментах решения учебной задачи, сформировать и
распространить алгоритм практических действий,
вовлечь полученные знания и приобретенные умения в обсуждение очередных проблем.
Все это позволяет приступить к осуществлению
одной из важнейших задач средней школы – образованию навыков поисковой деятельности учащихся.
Решение достаточно сложной для ученика
задачи можно рассматривать как бы в двух “плоскостях”: наблюдения и визуальный поиск.
Навык наблюдений сам по себе не приходит.
Он образуется в результате целенаправленной работы учителя и ученика.
Для формирования таких навыков полезны специальные упражнения.
Их можно составлять к каждому разделу курса, иногда предлагать комплекты заданий,
основанных на материалах различных тем. В последнем случае желательно, чтобы они
представляли собой единую модель, позволяли постепенно переходить от одного фрагмента
математической информации к другому.
Наблюдения в 9 классе школы № 34
г. Мурманска первый раз
было решено организовать на уроке по
теме “Графики функций y = xn nОN
(n принадлежит N)”.
Целью урока являлось знакомство учеников со степенной функцией (при натуральных
показателях степени).
Результатом этого урока планировалось образование у учеников нового навыка:
распознавания функций
графиковy = x2n и
y = x2n+1 при nОN
(n принадлежит N).
На повторение ушло 5 минут.
Работая по вариантам с матрицей (рис. 57),
записали ответы в первых двух строках, затем сверили результаты. Обсудили задания
четвертой строки, 3-я и 5-я строка
были заданы на дом.
Переход к новой теме начался с известного.
Вспомнили принципы построения графиков функций y = x, y = x2
и y = x3. При помощи наблюдений,
сопутствующих обсуждению графика функции y = x4, пришли
к заключению, что кривая, являющаяся
графиком этой функции, похожа на график функции y = x2,
а график функции y = x5 похож на график y = x3.
Правильность выводов проверили по (рис. 58-1).
Сделали обобщение: график функции y = x2n
при nО N
(n принадлежит N) строится по типу
графика функции y = x2, а график
y = x2n+1 – аналогично
графику y = x3 при nОN
(n принадлежит N).
Такие обобщения,
полученные в результате наблюдений,
позволили за один урок решить достаточно
большое количество различных задач, ориентированных на формирование намеченного
в цели урока навыка (рис. 58-2).
 Pис. 57 |
 Pис. 58-1 |
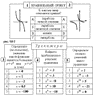 Pис. 58-2 |
Данная тема не входит в перечень обязательных.
Этот урок был осуществлен за счет резерва времени,
образовавшегося благодаря постоянному и целенаправленному
использованию подобных дидактических материалов, что совершенно
не исключает применение обычных учебных пособий и традиционных приемов обучения.
В 11 классе очень хорошо прошла трудная тема “Показательная и логарифмическая функции”. Было предложено много дополнительного материала, выстроенного в порядке возрастания сложности. Ученики быстро и свободно решали, например, показательные и логарифмические уравнения с модулем, логарифмические и показательные уравнения и неравенства повышенной сложности. Выпускную работу ученики написали честно, четко и грамотно. Многие решали задание повышенной сложности, изложив разные и нестандартные подходы.
Работа с подобными материалами
позволила понять, как можно добиться успеха
в обучении детей даже в условиях обычной школы, сохранить и развить их
природные способности и возможности.
Скачать комплект
визуальных дидактических материалов по теме данной статьи.
Предлагаемые комплекты дидактических материалов на экране отражаются не совсем точно,
но распечатываются рисунки прекрасно!
Уважаемые коллеги!
Мы с благодарностью примем
ваши замечания и предложения.
Наталья Резник (nareznik@yandex.ru),
Наталия Ежова (naegova@yandex.ru)